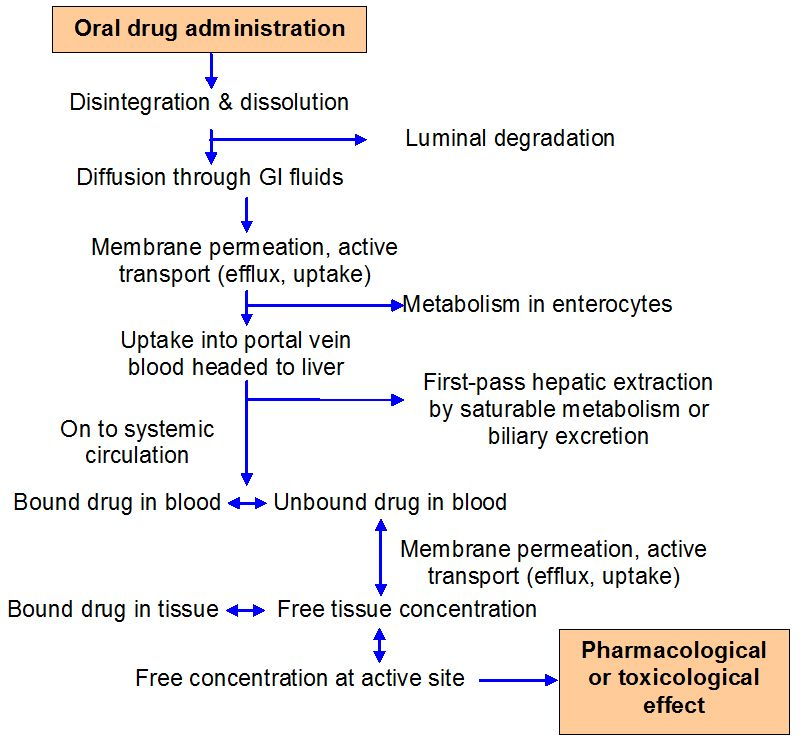
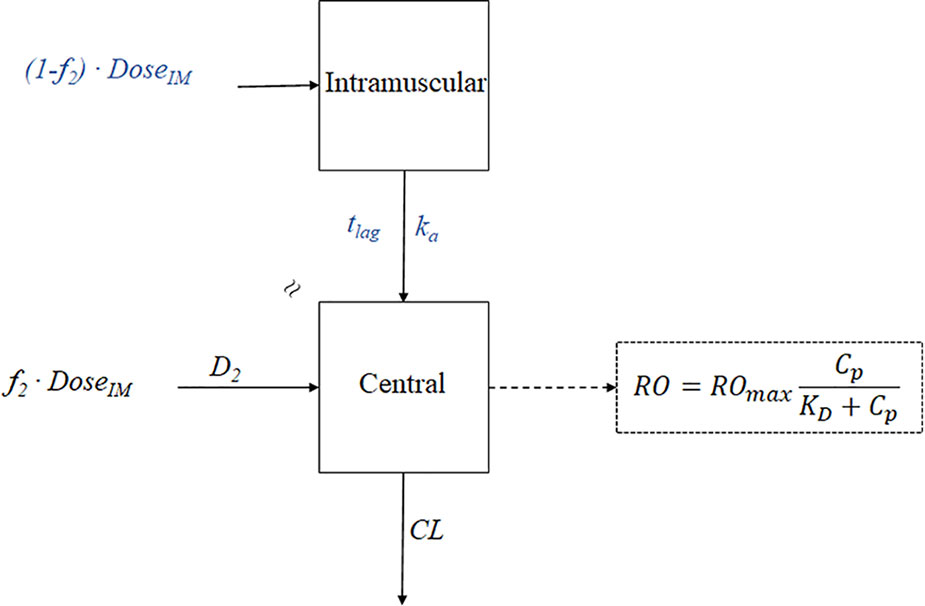
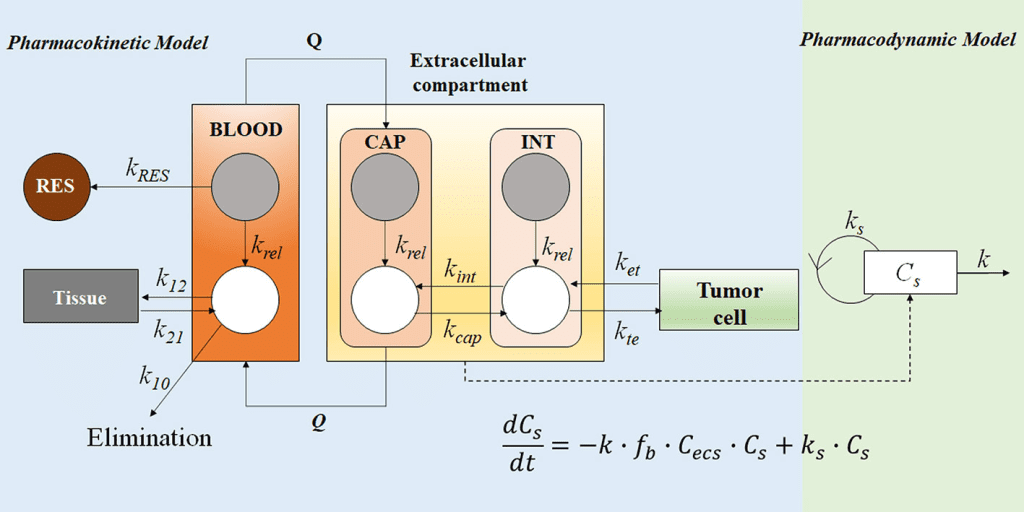
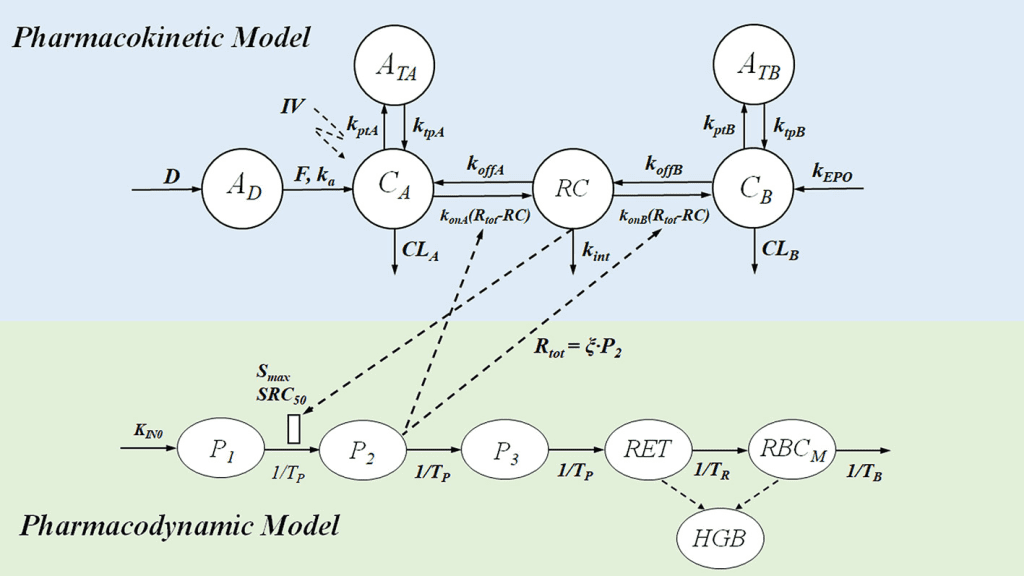
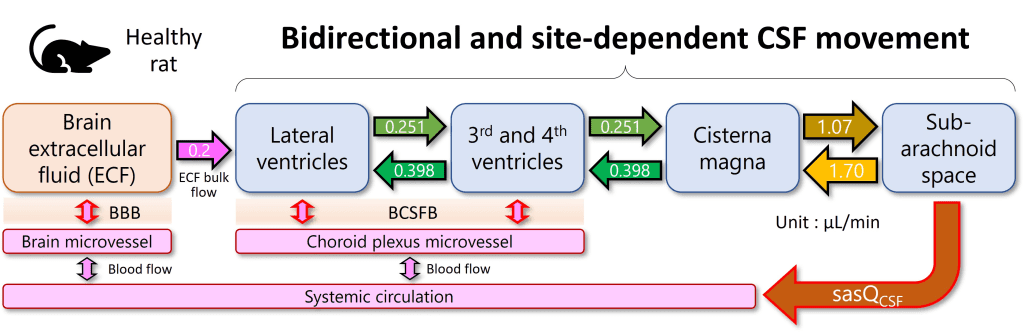
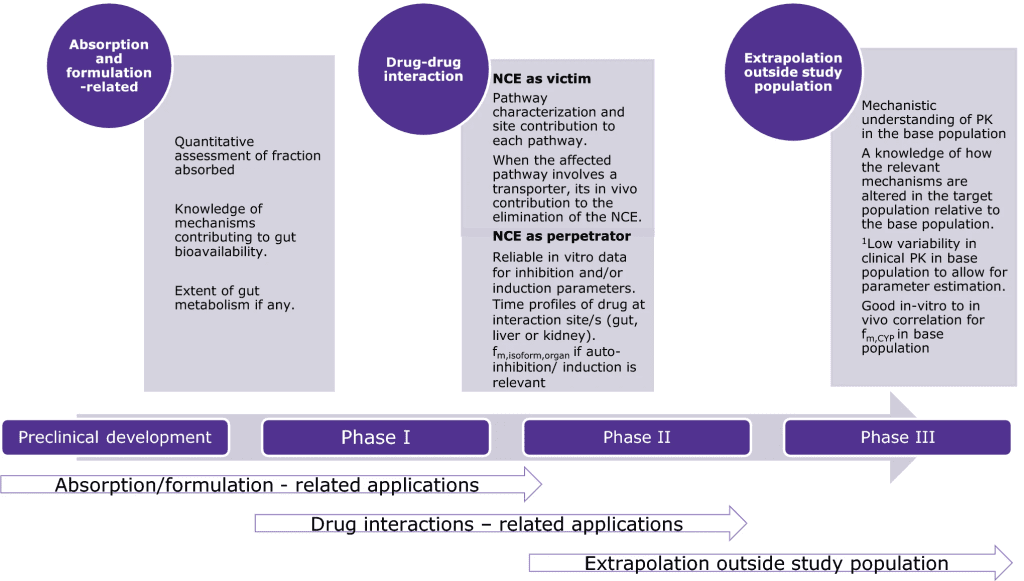
As drugs migrate between tissues and bodily fluids, bind to plasma or cellular components, or are digested, they are in a dynamic state within the body. The distribution and disposition of drugs in the body are complex processes, and many drug events take place at the same time. The design of pharmacological therapy regimens must take these considerations into account. To estimate drug dosage and anticipate the time course of treatment efficacy for a given dose, mathematical models and statistics must be used because of the innate and limitless complexity of these processes.
Mathematical Models and Basic Pharmacokinetics
A model is a conjecture that expresses quantitative connections succinctly in mathematical words.
The correct definition and formulation of mathematical function(s) that parameterize the crucial parameters regulating the kinetic process is what gives a model its predictive power. It is usual practice to estimate a process’s critical parameters by fitting the model to experimental data, also referred to as variables. A drug’s constant is known as a pharmacokinetic parameter, and it is estimated using experimental data. For instance, pharmacokinetic parameters like k that are estimated rely on the tissue sampling technique, sample time, drug analysis, and chosen predictive model.
An independent variable and a dependent variable are connected by a pharmacokinetic function, which frequently makes use of parameters. For instance, a pharmacokinetic model may forecast the drug concentration in the liver one hour following oral delivery of a 20-mg dose. Time is an independent variable, and drug concentration in the liver is a dependent variable. A model equation is developed to forecast the hepatic drug concentration with respect to time based on a set of time versus drug concentration data. In this instance, the time following the administration of the dose determines the drug concentration, and the time-concentration connection is described by the pharmacokinetic parameter k, or the elimination rate constant.
These mathematical models can be created to replicate the processes by which drugs are absorbed, distributed, and eliminated in order to characterize and forecast how drug concentrations change over time in the body. Pharmacokinetic models are employed to: (a) predict plasma, tissue, and urine drug levels with any dosage regimen; (b) determine the best dosage schedule for each patient; (c) estimate the potential accumulation of drugs and/or metabolites; (d) correlate drug concentrations with pharmacologic or toxicologic activity; (e) assess variations in the rate or extent of availability between formulations (bioequivalence); (f) explain how changes in physiology or disease can affect drug absorption; and (g) elaborate mechanisms of drug interactions.
In order to represent a complex biologic system regarding the circulation of medications within the body, pharmacokinetic models make simplifying assumptions. For instance, the majority of pharmacokinetic models make the assumption that the plasma drug concentration represents the drug concentrations throughout the body.
Types of Pharmacokinetic Models
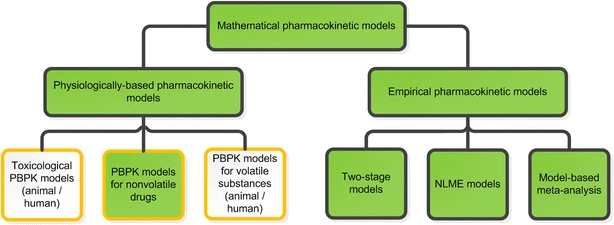
A model may be based on empirical, physiological, or compartmental data. When there is little information available, the model that merely interpolates the data and permits an empirical formula to estimate drug level over time is warranted. Although practical, empirical models are not particularly helpful in describing the mechanism of how a drug is actually taken, disseminated, and removed from the body.
Empirical or mechanistic models can be widely characterized. Empirical models are primarily concerned with explaining the data and specifying a minimum number of underlying assumptions. Allometric scaling, a method of PK parameter prediction across many species, is an example of an empirical model. While summarizing the available data, mechanistic models, on the other hand, specify assumptions and make an effort to incorporate known elements about the systems around the data into the model. The latter group encompasses both compartmental modeling and physiological modeling.
Models that are based on biology have their own drawbacks. Using the aforementioned example, the researcher needs to comprehend the following inquiries in addition to the necessity of sampling tissue and observing blood flow to the liver in vivo. What clinical consequences does the liver drug concentration value have? Should the drug concentration in the liver tissue be deducted from the drug concentration in the blood within the tissue? If a selective biopsy liver tissue sample can be obtained without contamination from its surroundings, what kind of cell is representative of the liver? Tissue medication concentrations can vary depending on distance to the blood artery or even the kind of cell in the liver, based on the spatial location of the liver tissue from the hepatic blood vessels. The medication concentration in the tissue will also change when the liver blood circulation changes. If heterogeneous liver tissue is homogenized and then analyzed, the homogenized tissue merely represents an average concentration of all the cells and blood present in the liver at the time of collection. Since it is impractical to homogenize tissue in human beings, the drug concentration in the liver can be inferred by understanding the liver extraction ratio for the drug and the physiologic and biochemical makeup of the other body organs.
To estimate regional and global data regarding drug disposal in the body, numerous models have been created.
Depending on the level of detail taken into consideration, an infinite number of models might theoretically be created to describe the kinetic processes of drug absorption, distribution, and elimination in the body. New pharmacokinetic models have grown quite slowly due to practical constraints.
Compartmentally based models are a very straightforward and practical pharmacokinetics technique. Consider the scenario when a medicine is administered intravenously and dissolves (distributes) quickly in body fluids. A tank carrying a volume of fluid which quickly equilibrates with the medication is one pharmacokinetic paradigm that can adequately depict this scenario. The fluid capacity of the tank that will dilute the drug and the drug’s rate of elimination per unit of time determine the concentration of the drug in the tank following a given dose. The one-compartment open model, a fluid-filled tank model, can frequently be used to illustrate a medication’s pharmacokinetic features even though it may provide an overly simplified understanding of drug disposition in the human body (see below). In both the tank and the one-compartment body model, a small amount of the medication would be continuously removed as time passed.
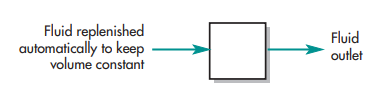
These variables are thought to be constant for a certain drug in pharmacokinetics. The volume of fluid in the tank or compartment (VD, volume of distribution) and the rate of drug clearance can be approximated if drug concentrations in the tank are evaluated at different times after delivery of a specified dosing.
In real life, medication concentrations are gathered throughout time and used as data to experimentally estimate pharmacokinetic parameters like k and VD. The intricacy of the process and the medication administration route determine the number of parameters required to define the model. In general, it gets harder and harder to estimate these parameters accurately the more parameters are needed to model the data. Computer algorithms are employed to simplify parameter estimate in complex pharmacokinetic models. The number of data points must always be more than the number of model parameters for the parameters to be considered valid.
When completely relying on the pharmacokinetic model to forecast drug activity, some degree of care is required because a model is based on a hypothesis and simplifying assumptions. Plasma drug concentrations for some medications are not reliable indicators of pharmacological action. For some medications, a person’s genetic makeup, level of illness, and body’s compensating mechanism may change how they react to the medication. A new, more complex model may be proposed and afterwards evaluated if a basic model is unable to adequately account for all of the experimental observations. Pharmacokinetic data should be interpreted with clinical observations rather than taking the place of the clinician’s sound judgment because few data are often available in most clinical scenarios.
The creation of pharmacometric statistical models may aid in improving the population’s ability to forecast medication levels among patients. It will take some time before these techniques are widely used, though.
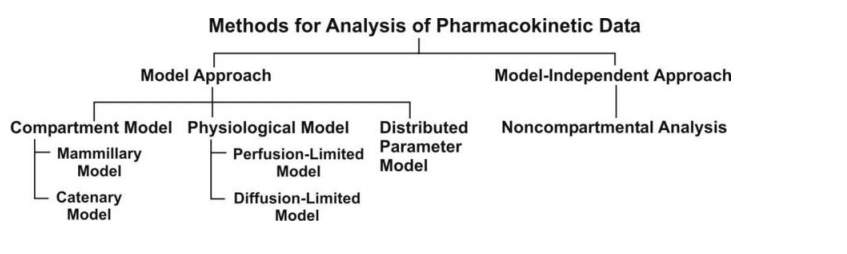
Compartment Models
Physiologic pharmacokinetic models, which are based on actual tissues and their related blood flow, accurately represent the data if the tissue drug concentrations and binding are known. Since tissue samples are readily available for analysis, physiologic pharmacokinetic models are widely employed to describe drug distribution in animals. However, as tissue samples from human individuals are frequently unavailable, the majority of physiological models make the assumption that each subject’s blood flow will be on average.
Contrarily, due to the body’s immense complexity, drug kinetics in the body are commonly simplified and represented by one or more tanks, or compartments, that can communicate with one another in a reversible fashion. A tissue or set of tissues that have comparable blood flow and drug affinities are referred to as compartments even if they are not actual physiologic or anatomical regions. The distribution of the medicine is thought to be uniform inside each compartment. In order for the drug concentration to represent an average concentration and for each drug molecule to have an equal chance of exiting the compartment, the drug must be quickly and uniformly mixed within the compartment, a process known as “well stirring.” The total rate processes of drugs entering and leaving the compartment are represented by rate constants. Because drugs can be removed from the system, the model is an open system. Compartment models are based on linear differential equations and linear assumptions.
Mamillary Model
Drugs go to and from the central or plasma compartment through one or more compartments that are easily created using a compartmental model. The most used compartment model in pharmacokinetics is the mammillary model. The mammillary model is a strongly coupled system because, following drug introduction into a specific compartment, one may estimate the amount of drug present in any compartment of the system. Drug is added to and removed from a central compartment in the one-compartment concept. Plasma and highly perfused tissues that quickly equilibrate with medication are designated to represent the core compartment. Drugs administered intravenously enter the central compartment right away. Because the primary organs involved in drug elimination, the kidney and liver, are well-perfused tissues, drug clearance takes place from the central compartment.
Drug can travel to and from the tissue compartment in a two-compartment model by passing via the central or plasma compartment. Even though no particular tissue is represented by the tissue compartment, the mass balance takes into consideration the medication that is available in all tissues. According to this approach, the sum of the drug present in the central compartment and the drug accessible in the tissue compartment is all the drug that exists in the body. One may calculate the amount of drug still in the body and the amount of drug being removed from the body at any time by knowing the parameters of either the one-compartment or the two-compartment model. When scant data about the tissues is available, compartmental models are especially helpful.
In the diagram below, many compartment model types are described.
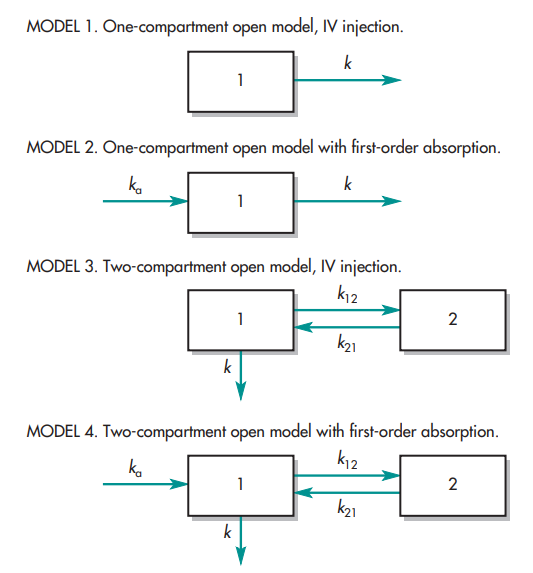
The letter k stands for the pharmacokinetic rate constants. The center or plasma compartment is represented by compartment 1, while the tissue compartment is represented by compartment 2. Three purposes are served by model drawings. The model: (1) provides a pictorial depiction of the rate processes; (2) illustrates the number of pharmacokinetic constants required to adequately describe the process; and (3) affords the pharmacokineticist to compose differential equations to characterize drug permeation variations in each compartment.
The volume of the compartment and the elimination rate constant, k, are the two parameters required to describe model 1. The volumes of compartments 1 and 2 and the rate constants ka, k, k12, and k21 make up the six pharmacokinetic parameters in the instance of model 4.
It is crucial to understand whether drug concentration data can be directly taken from each compartment when analyzing these models. For models 3 and 4, data for compartment 2 cannot be readily produced since tissues are difficult to sample and could not have uniform drug concentrations. The amount of drug present in tissue compartment 2 can be mathematically approximated if the amount of medication absorbed and eliminated per unit time is determined by sampling compartment 1.
Catenary Model
The catenary model and the mammillary model are two different kinds of compartmental models used in pharmacokinetics. Compartments connected to one another like train cars make up the catenary model.
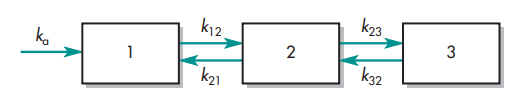
The mammalian model, in contrast, has satellite-like compartments that surround a core compartment. The catenary model is less frequently employed than the mammillary model because it fails to account for the direct connections between the majority of the body’s functional organs and the plasma.
Physiologic Pharmacokinetic Model (Flow Model)
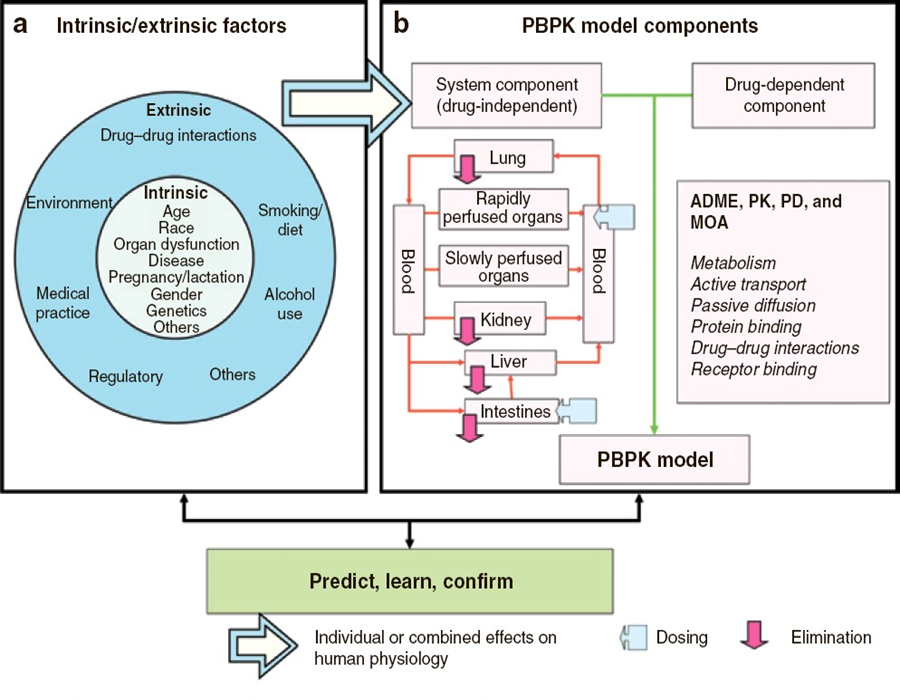
Pharmacokinetic models based on anatomical and physiological knowledge are referred to as physiological pharmacokinetic models, often known as blood flow or perfusion models. Since that blood flow is what distributes drugs to the body’s various regions, the models explain the data kinetically. Drug binding in these tissues controls how quickly a drug enters an organ. The actual tissue volume is utilized as opposed to an approximated tissue volume of distribution. Because the body contains numerous tissue organs, each tissue volume should be measured and its medication concentration must be specified. The two-compartment model is unable to predict realistic tissue drug concentrations, but the proposed model might. Unfortunately, it is challenging to gather enough data experimentally to fully describe a physiologic pharmacokinetic model. The physiologic pharmacokinetic model does, however, offer a far better understanding of how physiologic variables may alter drug distribution from one animal species to another despite this shortcoming. Here is a list of further significant variations.
The perfusion model does not require any data fitting, to start. Blood flow, organ tissue size, and experimentally determined drug tissue-blood ratios all help predict drug concentrations in different tissues (i.e., partition of drug between tissue and blood). Second, due to certain pathophysiologic conditions, blood flow, tissue size, and medication tissue-blood ratios may differ. Hence, physiologic pharmacokinetic models must account for the impact of these changes on drug distribution. Thirdly, and perhaps most significantly, physiologically based pharmacokinetic models can be used to predict drug responses in a variety of species and, for some medications, extrapolate results from human subjects. Since the compartment models’ volume of distribution is a mathematical construct rather than a simple relationship between blood volume and blood flow, extrapolating from animal data to them is not conceivable. To date, perfusion models have been used to describe a wide range of medications, such as digoxin, lidocaine, methotrexate, and thiopental. Although compartment models generally do a good job of describing blood levels, several of these medications cannot be assumed to be present in tissues. This is a diagram illustrating a perfusion model.
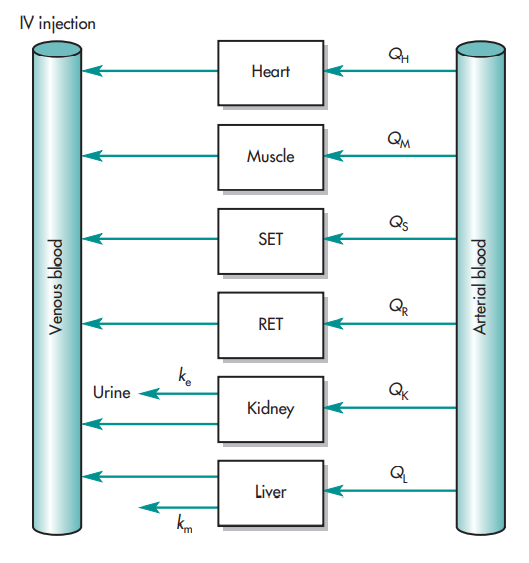
The ks stand for kinetic constants, with km being the rate constant for hepatic elimination and ke being the first-order rate constant for urinary drug excretion. The “boxes” are actually tissue compartments. Organs that play a significant role in drug absorption are taken into account individually, while other tissues are categorized as RET (rapidly equilibrating tissue) and SET (slowly equilibrating tissue). Instead of being estimated mathematically, the size or mass of each tissue compartment is calculated physiologically. The rate of blood perfusion to the tissue, denoted by Q, and the tissue’s capacity to accumulate drug both affect the concentration of the drug in the tissue.
A perfusion model’s tissue compartment count varies depending on the medication. Normally, tissues or organs with no drug penetration are not taken into account. As a result, organs including the brain, bones, and other areas of the central nervous system are frequently left out of therapeutic trials because most medications barely penetrate these tissues. The model may become extremely complex and mathematically challenging if each organ were to be described independently by a differential equation. Grouping all the tissues with comparable blood perfusion characteristics into a single compartment is a less complex but still effective strategy.
In order to represent the distribution of lidocaine in blood and different organs, a physiologic based pharmacokinetic model (PBPK) employing known blood flow was employed in anesthesia in humans. In PBKB models, tissues were occasionally categorized as RET (rapidly equilibrating tissue) and SET (slowly equilibrating tissue) for convenience to account for the mass balance of the drug. Organs such as the lung, liver, brain, and muscle were independently modeled by differential equations.
Based on this physiologic model, drug levels in various organs could be accurately predicted and scaled to humans. Due to the reduced blood flow, tissues like adipose (fat) tissue take longer to absorb medicines like lidocaine. Contrarily, vascular tissues, such as the lung, quickly equilibrate with the blood and begin to diminish as soon as the blood drug level begins to decline, causing a curve in the plasma profile. The physiologic pharmacokinetic model offers a realistic way to simulate drug levels in tissue. Drug levels in tissues, however, are not known. There have been widespread complaints about physiologic pharmacokinetic models since there aren’t as many data points as there are parameters. The projected data are therefore not sufficiently limited.
The physiologically based model’s potential use in predicting human pharmacokinetics from animal data is what gives it its true significance. It is frequently known or possible to calculate the mass of various body organs or tissues, the degree of protein binding, the capacity for drug metabolism, and blood flow in humans and other species. In circumstances where human beings are involved, physiologic and anatomic factors can be used to anticipate the effects of medications on humans from the effects on animals. Experimentation is challenging or constrained.
As our understanding of human and animal physiology advances, more complex models are developed, such as compartmentalized models that account for the transporter-mediated drug disposition of certain medicines. Physiologic Pharmacokinetic Model Including Hepatic Transporter-Mediated Clearance is the name of this method. The mass transfer and medication balances in and out of the body or bodily organs are essentially a kinetic process, it is vital to highlight. In light of the identification of all drugs transported to body organs, the model may be referred to as biologically based. Parameters are quantitatively determined for data analysis under various assumptions. Either a compartmental or noncompartmental model analysis is possible. One strategy is to categorize models simply as mechanistic models and models based on empirical data. Although being criticized as a “black box” methodology and not physiological, compartment models are still widely used. Compartment models’ adaptability and simplicity of use are based on basic mass transport algorithms or a set of differential equations. This method has made it possible to track numerous bodily functions, including binding, transport, and metabolic clearance.
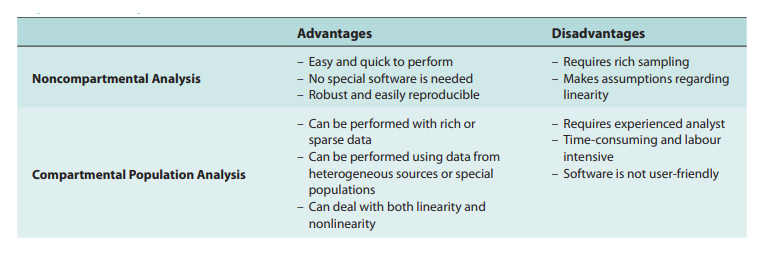
Population Analyses
Frequently Asked Questions (FAQs)
Why are drug concentrations more often measured in plasma rather than whole blood or serum?
Plasma and red blood cells (RBCs) make up blood. The liquid extracted from blood after it has clots is called serum. Protein composition varies between serum and plasma. RBCs can be viewed as a cellular component of the body where the drug concentration in the serum or plasma is in equilibrium, similar to how this is the case with the body’s other tissues. Compared to serum or plasma samples, whole blood samples are typically more difficult to prepare and analyze. The fluid in the plasma can be thought of as a liquid tissue compartment where the drug equilibrates with the drug in the tissues and cellular components.
At what time intervals should plasma drug concentration be taken in order to best predict drug response and side effects?
For the majority of medications, the precise site of pharmacological action is uncertain. From research on the relationship between the time course for the drug concentration and the pharmacodynamic effect, the length of time required for the drug to reach the site of action, generate a pharmacodynamic effect, and reach equilibrium is inferred. When the drug has been distributed and reached equilibrium, the drug concentration is frequently measured during the elimination phase. The peak and trough medication concentrations are routinely measured for investigations involving numerous doses..
What are the reasons to use a multicompartment model instead of a physiologic model?
Comparatively to compartment models, physiological models are more sophisticated and call for more data to make reliable predictions. The physiologic model will be biased or mistaken if certain details are missing. Compartment models are less complex since they take for granted that medication concentrations in the arterial and venous blood are comparable. The compartment model takes into account a faster phase of distribution and a more gradual phase of elimination. Drug levels in arterial blood are thought to be higher than those in venous blood, according to physiological clearance models. Only venous blood samples are typically taken in practice. The diagnosis of some disorders involving arterial perfusion and the treatment of tumors both benefit from an understanding of organ medication clearance. The use of physiological models in a broad sense is challenging.
Engr. Dex Marco Tiu Guibelondo, B.Sc. Pharm, R.Ph., B.Sc. CpE
Editor-in-Chief, PharmaFEATURES

Subscribe
to get our
LATEST NEWS
Related Posts

Medicinal Chemistry & Pharmacology
Pathogenic Targeting 5.0: The Rise of RNA Therapeutics and Peptide-Based Drugs in Modern Medicine
Unlike traditional small-molecule drugs, which interact with proteins, RNA therapies modulate gene expression directly, enabling interventions at the root of disease.

Medicinal Chemistry & Pharmacology
Polarity Alchemy: Strategic Charge Manipulation in Contemporary Drug Design
The future promises tunable therapies with polarity adjustable by light, magnetic fields, or bioorthogonal triggers.
Read More Articles
Mini Organs, Major Breakthroughs: How Chemical Innovation and Organoids Are Transforming Drug Discovery
By merging chemical innovation with liver organoids and microfluidics, researchers are transforming drug discovery into a biologically precise, patient-informed, and toxicity-aware process.
Tetravalent Vaccines: The Power of Multivalent E Dimers on Liposomes to Eliminate Immune Interference in Dengue
For the first time, a dengue vaccine candidate has demonstrated the elusive trifecta of broad coverage, balanced immunity, and minimal enhancement risk,